CBSE Class 12 Maths Sample Paper 2022-23

We have shared CBSE Class 12 Maths Sample Paper 2023 to help all the board-appearing candidates with the weightage, design, and questions asked during the board examination.

Revision is the key to Learning and for that CBSE has introduced Sample Papers for classes 10th and 12th to give a nice practice and revision to the candidates who want a good percentage.

We have shared CBSE Class 12 Maths Sample Paper 2022-23 pdf along with CBSE Class 12 Maths Sample Paper 2022-23 Marking Scheme to help you all with the sample papers and the accurate solutions. Students can download it from the link given below and practice them to boost their understanding and learning.

Contents

CBSE Class 12 Maths Sample Paper 2022-23

•Time Allowed: 3 Hours

•Maximum Marks: 80
General Instructions :
1. This Question paper contains – five sections A, B, C, D, and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section A has 18 MCQs and 02 Assertion-Reason-based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA)-type questions of 2 marks each.
4. Section C has 6 Short Answer (SA)-type questions of 3 marks each.
5. Section D has 4 Long Answer (LA)-type questions of 5 marks each.
6. Section E has 3 sources based/case based/passage based/integrated units of assessment (4 marks each) with sub-parts.

Class 12 Maths Sample Question Paper 2023-SECTION A

SECTION A
(Multiple Choice Questions)
Each question carries 1 mark

Q1. If A =[aij] is a skew-symmetric matrix of order n, then
(a) 𝑎ij=1/aij ∀ 𝑖,𝑗 (b)𝑎ij≠ 0 ∀ 𝑖,𝑗 (c)𝑎ij = 0 where 𝑖=𝑗 (d) 𝑎ij≠ 0 where i=j

Q2. If A is a square matrix of order 3, |𝐴′| = −3, then |𝐴𝐴′| =
(a) 9 (b) -9 (c) 3 (d) -3
Q3. The area of a triangle with vertices A, B, and C is given by

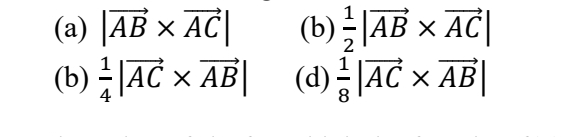
Q4. The value of ‘k’ for which the function

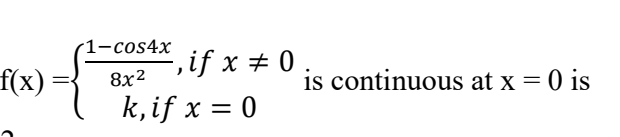
(a) 0 (b) -1 (c) 1. (d) 2
Q5. If 𝑓'(𝑥) = 𝑥 + 1/x, then 𝑓(𝑥) is
(a) 𝑥²+ log |𝑥| + 𝐶 (b) 𝑥²/2 + log |𝑥| + 𝐶 (c) 𝑥/2 + log |𝑥| + 𝐶 (d) 𝑥/2− log |𝑥| + 𝐶
Q6. If m and n, respectively, are the order and the degree of the differential equation

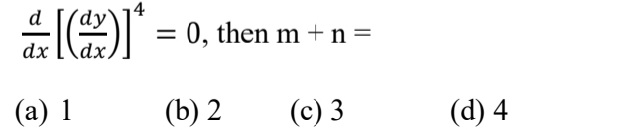
Q7. The solution set of the inequality 3x + 5y < 4 is
(a) an open half-plane not containing the origin.
(b) an open half-plane containing the origin.
(c) the whole XY-plane not containing the line 3x + 5y = 4.
(d) a closed half-plane containing the origin.

Q.8.The scalar projection of the vector 3𝚤̂− 𝚥̂− 2k̂ on the vector 𝚤̂+2𝚥̂-3k̂ is

(a) 7/√14 (b) 7/14 (c) 5/13 (d) 7/2

Q.9.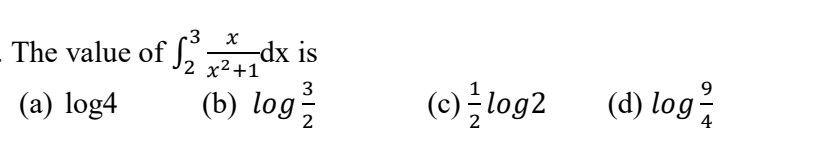

Q10. If A and B are non-singular square matrices of the same order, then (𝐴𝐵-¹)-¹
(a)𝐴–¹B (b)𝐴–¹B–¹ (c)𝐵𝐴–¹ (d) 𝐴𝐵
Q11. The corner points of the shaded unbounded feasible region of an LPP are (0, 4),(0.6, 1.6) and (3, 0) as shown in the figure. The minimum value of the objective function Z = 4x + 6y occurs at

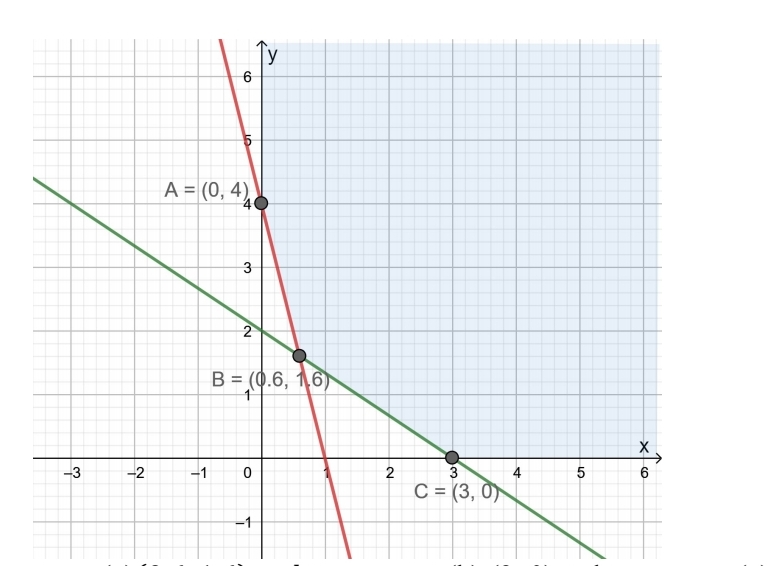
(a)(0.6, 1.6) 𝑜𝑛𝑙𝑦 (b) (3, 0) only (c) (0.6, 1.6) and (3, 0) only
(d) at every point of the line-segment joining the points (0.6, 1.6) and (3, 0)

Q12.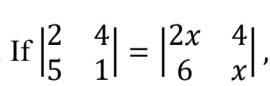

𝑡ℎ𝑒𝑛 𝑡ℎ𝑒 𝑝𝑜𝑠𝑠𝑖𝑏𝑙𝑒 value(s) of ‘x’ is/are

(a) 3 (b) √3 (c) -√3 (d) √3, −√3
Q13. If A is a square matrix of order 3 and |A| = 5, then |𝑎𝑑𝑗𝐴| =
(a) 5 (b) 25 (c) 125 (d) 1/5

Q14. Given two independent events A and B such that P(A) =0.3, P(B) = 0.6, and P(𝐴’∩ 𝐵’) is
(a) 0.9 (b) 0.18 (c) 0.28 (d) 0.1
Q15. The general solution of the differential equation 𝑦𝑑𝑥 − 𝑥𝑑𝑦 = 0 𝑖𝑠
(a) 𝑥𝑦 = 𝐶 (b) 𝑥 = 𝐶𝑦²
(c) 𝑦 = 𝐶𝑥 (d) 𝑦 = 𝐶𝑥²
Q16. If 𝑦 = 𝑠𝑖𝑛–¹𝑥, then (1 − 𝑥²)y2 𝑖𝑠 equal to
(a) 𝑥𝑦1 (b) 𝑥𝑦 (c) 𝑥𝑦2 (d) 𝑥²
Q17. If two vectors 𝑎⃗ 𝑎𝑛𝑑 𝑏are such that |𝑎⃗| = 2 ,|b→| = 3 𝑎𝑛𝑑 𝑎⃗. b→= 4,𝑡ℎ𝑒𝑛 |𝑎⃗ − 2b→| is equal to
(a) √2 (b) 2√6 (c) 24 (d) 2√2
Q18. P is a point on the line joining the points 𝐴(0,5, −2) and 𝐵(3, −1,2). If the x-coordinate of P is 6, then its z-coordinate is
(a) 10 (b) 6 (c) -6 (d) -10

ASSERTION-REASON BASED QUESTIONS

In the following questions, a statement of assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.

Class 12 Maths Sample Paper 2022-23-SECTION B

SECTION B
This section comprises very short answer type-questions (VSA) of 2 marks each

Q.21.Find the Value of

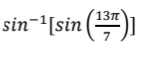
OR
Prove that the function f is surjective, where 𝑓: 𝑁 → 𝑁 such that

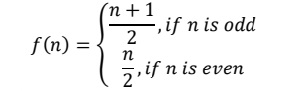
Is the function injective? Justify your answer.
Q22. A man 1.6 m tall walks at the rate of 0.3 m/sec away from a street light that is 4 m above the ground. At what rate is the tip of his shadow moving? At what rate is his shadow lengthening?

Q23. If 𝑎⃗ = 𝚤̂− 𝚥̂+ 7k̂ and b→= 5𝚤̂− 𝚥̂+ 𝜆k̂, then find the value of 𝜆 so that the vectors
𝑎⃗ + b→ 𝑎𝑛𝑑 𝑎⃗ − 𝑏→ are orthogonal.

Find the direction ratio and direction cosines of a line parallel to the line whose equations are

6𝑥 − 12 = 3𝑦 + 9 = 2𝑧 − 2

Q24. If 𝑦√(1 − 𝑥²) + 𝑥√(1 − y²) = 1 ,𝑡ℎ𝑒𝑛 𝑝𝑟𝑜𝑣𝑒 𝑡ℎ𝑎𝑡

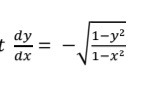
Q25. Find |𝑥⃗| if (𝑥⃗ − 𝑎⃗). (𝑥⃗ + 𝑎⃗) = 12, where 𝑎⃗ is a unit vector.

Class 12 Maths Sample Paper 2022-23-SECTION C

SECTION C
(This section comprises short answer type questions (SA) of 3 marks each)

Q26.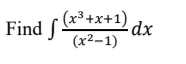

Q27. Three friends go for coffee. They decide who will pay the bill, by each tossing a coin and then letting the “odd person” pay. There is no odd person if all three tosses produce the same result. If there is no odd person in the first round, they make the second round of tosses and they continue to do so until there is an odd person. What is the probability that exactly three rounds of tosses are made?
OR
Find the mean number of defective items in a sample of two items drawn one-by-one without replacement from an urn containing 6 items, which include 2 defective items. Assume that the items are identical in shape and size.

Q28.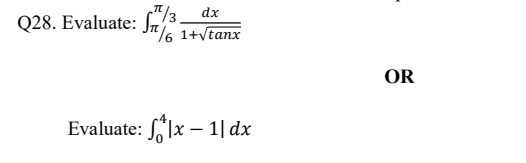

Q29. Solve the differential equation: 𝑦𝑑𝑥 + (𝑥 − 𝑦²)𝑑𝑦 = 0

OR
Solve the differential equation: 𝑥𝑑𝑦 − 𝑦𝑑𝑥 = √(𝑥²+ 𝑦²) 𝑑x

Q30. Solve the following Linear Programming Problem graphically:
Maximize Z = 400x + 300y subject to 𝑥 + 𝑦 ≤ 200, 𝑥 ≤ 40, 𝑥 ≥ 20, 𝑦 ≥ 0

Q31.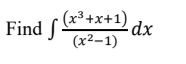

Class 12 Maths Sample Paper 2022-23-SECTION D

(This section comprises long answer-type questions (LA) of 5 marks each)

Q32. Make a rough sketch of the region {(𝑥, 𝑦): 0 ≤ 𝑦 ≤ 𝑥², 0 ≤ 𝑦 ≤ 𝑥, 0 ≤ 𝑥 ≤ 2} and find the area of the region using integration.
Q33. Define the relation R in the set 𝑁 × 𝑁 as follows:
For (a, b), (c, d) ∈ 𝑁 × 𝑁, (a, b) R (c, d) if ad = bc. Prove that R is an equivalence relation in 𝑁 × 𝑁.

OR,

Given a non-empty set X, define the relation R in P(X) as follows:
For A, B ∈ 𝑃(𝑋), (𝐴, 𝐵) ∈𝑅 iff 𝐴 ⊂ 𝐵. Prove that R is reflexive, transitive, and symmetric.

Q,34. An insect is crawling along the line 𝑟̅ = 6𝚤̂ + 2𝚥̂ + 2k̂ + 𝜆(𝚤̂ − 2𝚥̂ + 2k̂ )and an insect is crawling along the line 𝑟̅ = −4𝚤̂ − k̂ + 𝜇(3𝚤̂ − 2𝚥̂ − 2k̂). At what points on the lines should they reach so that the distance between them is the shortest? Find the possible distance between them.
OR
The equations of motion of a rocket are 𝑥 = 2𝑡, 𝑦 = −4𝑡, 𝑧 = 4𝑡, where the time t is given in seconds and the coordinates of a moving point in km. What is the path of the rocket? At what distances will the rocket be from the starting point O(0, 0, 0) and from the following line in 10 seconds?

𝑟̅ = 20𝚤̂ −10𝚥̂ +40k̂ + 𝜇(10𝚤̂ − 20𝚥̂ + 10 k̂)

Q.35.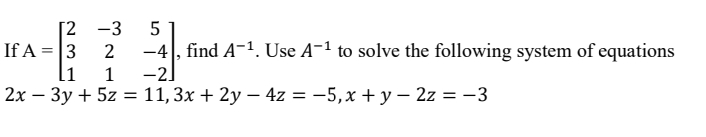

Class 12 Maths Sample Paper 2022-23-SECTION E

(This section comprises 3 case-study/passage-based questions of 4 marks each with two sub-parts. First, two case study questions have three sub-parts (i), (ii), (iii) of marks 1, 1, and 2 respectively. The third case study question has two sub-parts of 2 marks each.)

Q36. Case Study 1: Read the following passage and answer the questions given below.

The temperature of a person during an intestinal illness is given by

f(x) = -0.1x²+mx + 98.6,0 ≤ x ≤ 12, m being a constant, where f(x) is the temperature in °F at x days.

(i) Is the function differentiable in the interval (0, 12)? Justify your answer.

(ii) If 6 is the critical point of the function, then find the value of the constant m.

(iii) Find the intervals in which the function is strictly increasing/strictly decreasing.

(iii)Find the points of local maximum/local minimum, if any, in the interval (0, 12) as well as the points of absolute maximum/absolute minimum in the interval [0, 12]. Also, find the corresponding local maximum/local minimum and the absolute maximum/absolute minimum values of the function.

Q37. Case Study 2: Read the following passage and answer the questions given below.

For an elliptical sports field, the authority wants to design a rectangular soccer field with the maximum possible area. The sports field is given by the graph of x²/a²+ y²/b²= 1.

(i) If the length and the breadth of the rectangular field be 2x and 2y respectively, then find the area function in terms of x.

(ii) Find the critical point of the function.

(iii) Use the First derivative Test to find the length 2x and width 2y of the soccer field (in terms of a and b) that maximize its area.

(iii)Use Second Derivative Test to find the length 2x and width 2y of the soccer field (in terms of a and b) that maximize its area.

Q.38.Case-Study 2: Read the following passage and answer the questions given below.

There are two antiaircraft guns, named as A and B. The probabilities that the shell fired from them hit an airplane are 0.3 and 0.2 respectively. Both of them fired one shell at an airplane at the same time.

(i) What is the probability that the shell fired from exactly one of them hit the plane?

(ii) If it is known that the shell fired from exactly one of them hit the plane, then what is the probability that it was fired from B?

Class 12 Maths Sample Paper 2022-23 Pdf

We have provided you the link to the Class 12 Maths Sample Paper 2022-23 Pdf to practice.

https://drive.google.com/file/d/1S3MSZQszW_p99YJfN3kjTx7YdKCnxIMK/view?usp=sharing

Class 12 Maths Sample Paper 2022-23 Marking Scheme

We have shared the Class 12 Maths Sample Paper 2022-23 Marking Scheme to help you all with the solutions after you have practiced the sample paper.

https://drive.google.com/file/d/1SDRT6vcWEhxpOJ9cCQjEFOiQCi_DW8R9/view?usp=sharing

Conclusion

We have shared CBSE Class 12 Maths Sample Paper 2022-23 pdf along with CBSE Class 12 Maths Sample Paper 2022-23 Marking Scheme to help you all with the sample papers and the accurate solutions. Students can download it from the link given below and practice them to boost their understanding and learning.

Related Articles