Ncert Solutions Class 10th Polynomials
Polynomials: Class 10th Chapter 2 Introduction
Polynomial
An algebraic expression in which the exponents of the variables are non-negative integers
is called polynomials. For example, 3x
4 + 2x
3 + x + 9, 3x 4 etc are polynomials.
Constant polynomial: A constant polynomial is of the form , where k is a real
number. For example, –9, 10, 0 are constant polynomials.
Zero polynomial: A constant polynomial ‘0’ is called a zero polynomial.
The general form of a polynomial:
A polynomial of the form where are
constants and.
Here are the respective coefficients of and n is the power of the
variable x. and are called the terms of p(x).
Classification of polynomials based on the number of terms
A polynomial having one term is called a monomial e.g. 3x, 25t 3 etc.
A polynomial having two terms is called a binomial e.g. 2t – 6, 3x 4 + 2x etc.
A polynomial having three terms is called a trinomial. e.g. 3x 4 + 8x + 7 etc.
Degree
The degree of a polynomial is the highest exponent of the polynomial variable. For
example, the degree of polynomial 3x
4 + 2x
3 + x + 9 is 4.
The degree of a polynomial term is the value of the exponent of the term.
Classification of polynomial according to their degrees
A polynomial of degree one is called a linear polynomial e.g. 3x + 2, 4x, x + 9.
A polynomial of degree two is called a quadratic polynomial. e.g. x
2 + 9, 3x
2 + 4x + 6 .
A polynomial of degree three is called a cubic polynomial e.g. 10x
3 + 3, 9x 3.
Note: The degree of a non-zero constant polynomial is zero, and the degree of a zero
polynomial is not defined.
Values of polynomials at different points
A polynomial is made up of constants and variables. Hence, the value of the polynomial
changes as the value of the variable in the polynomial changes. Thus, for the different
values of the variable x, we get different values of the polynomial.
Example:
Find the value of the polynomial at x = –2.
Solution:
The variable in the given polynomial is x. Hence, replacing x by ‒2.
p (x) = 3x
3 + 2x + 9
∴ p (–2) = 3 (–2)3 + 2 (–2) + 9
= –24 – 4 + 9
= –19
Zeroes of a polynomial
A real number a is said to be the zero of polynomial p(x) if p(a) = 0. In this case, a is also
called the root of the equation p(x) = 0.
Note:
The maximum number of roots of a polynomial is less than or equal to the degree of the
polynomial.
A non-zero constant polynomial has no zeroes.
A polynomial can have more than one zero.
Class 10 Maths NCERT Solutions Chapter 2 Polynomials Ex 2.1
Question 1:
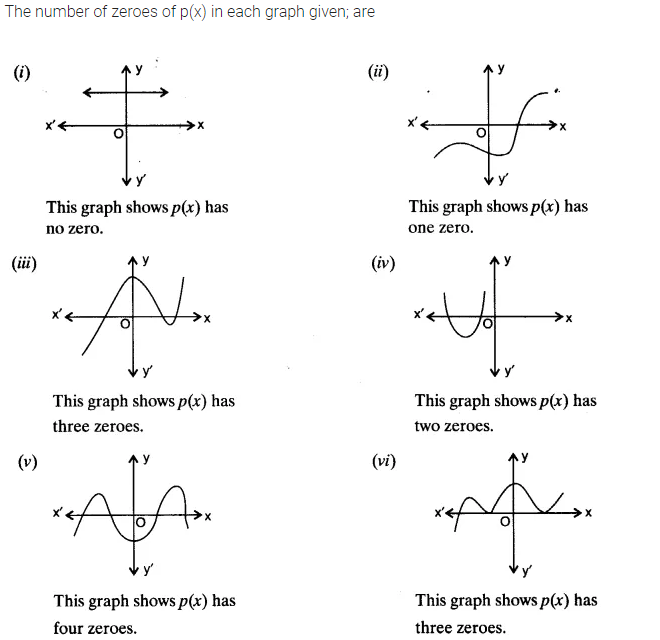
The graphs of y = p(x) are given below for some polynomials p(x). Find the number of zeroes of p(x) in each case.
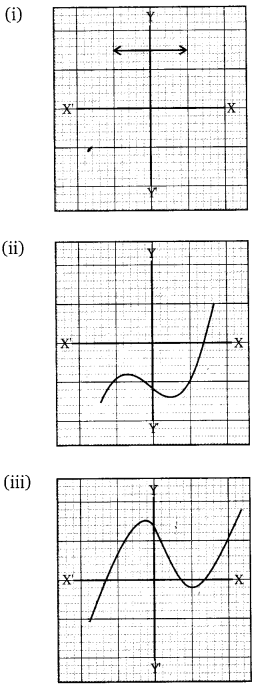
Solution:
Class 10 Maths NCERT Solutions Chapter 2 Polynomials Ex 2.2
Question 1.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and their coefficients:
(i) x2 – 2x – 8
(ii) 4s2 – 4s + 1
(iii) 6x2 – 3 – 7x
(iv) 4u2 + 8u
(v) t2 – 15
(vi) 3x2 – x – 4
Solution:

Question 2.
Find a quadratic polynomial, each with the given numbers as the sum and product of zeroes, respectively:
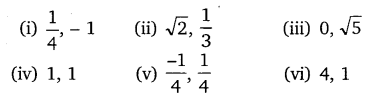

Class 10 Maths NCERT Solutions Chapter 2 Polynomials Ex 2.3
Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
(ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii) p(x) = x4– 5x + 6, g(x) = 2 – x2

Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
(i) t2 – 3, 2t4 + 3t3 – 2t2– 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x2 + 3x + 1, x5 – 4x3 + x2 + 3x + 1
Solution:

Question 3.
Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are and 53−−√ and –53−−√
Solution:

Question 4.
On dividing x3 – 3x2 + x + 2bya polynomial g(x), the quotient and remainder were x – 2 and -2x + 4 respectively. Find g(x).
Solution:
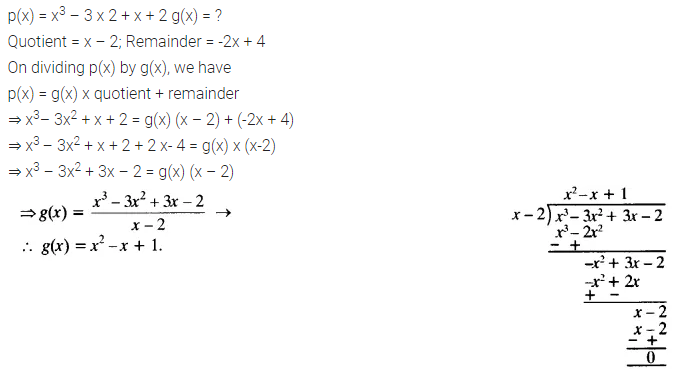
Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and:
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:
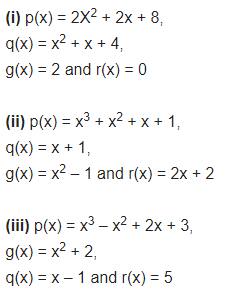
Class 10 Maths NCERT Solutions Chapter 2 Polynomials Ex 2.4
Question 1.
Verify that the numbers given alongside the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3 + x2 – 5x + 2; 14, 1, -2
(ii) x3 – 4x2 + 5x – 2; 2, 1, 1
Solution:

Question 2.
Find a cubic polynomial with the sum, some of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14, respectively.
Solution:
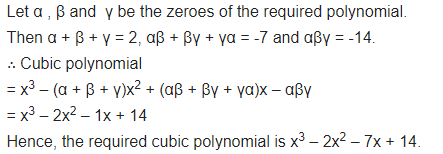
Question 3.
If the zeroes of the polynomial x3 – 3x2 + x + 1 are a-b, a, a + b, find a and b.
Solution:
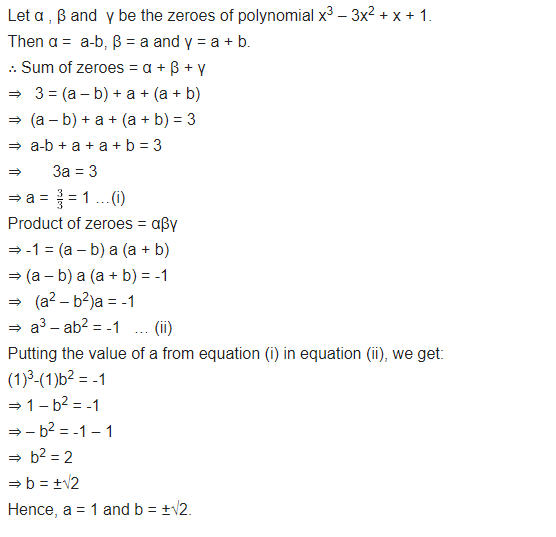
Question 4.
If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ± √3, find other zeroes.
Solution:

Question 5.
If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
Solutions:

Conclusion
We have shared all about Polynomials class 10th chapter along with the ncert solutions of Polynomials class 10th to help the students know the chapter and the tactics to attempt infinite questions on polynomials.
