Linear Equations In Two Variable Class 9th Maths

We are sharing an article related to Linear Equations In Two Variable Class 9th Maths, along with some critical points to remember and NCERT Solutions for class 9th Linear equations in Two variable to give a better understanding of the chapter linear equations class 9th to the students to improve their accuracy and give them the idea of plotting graphs.
Linear Equations In Two Variable Class 9th Maths: Introduction
A simple linear equation is a statement of equality between two algebraic expressions involving an unknown quantity called the variable. In a linear equation, the power of the variable is always equal to 1. The two sides of an equation are called Left-Hand Side (LHS) and Right Hand Side (RHS). They are written on either side of the equality sign.
 Equations of Condition
Equations of Condition
Study the following equations:
(a) 4x + 2 = 14
(b) x – 7 = 5 – 2x
(c) 3a – 8 = a + 12
The equation 4x + 2 = 14 is true only when x = 3,
Similarly, x – 7 = 5 – 2x is true only when x = 4, and
3a – 8 = a + 12 is true only when a = 10.
The two expressions (LHS and RHS) are equal only for a particular value of the variable x.
These equations are called equations of condition.
Identical Equations or Identities
Now study the equations given below:
(a) x + 3 + x + 4 = 2x + 7
2x + 7 = 2x + 7 (By simplification)
[any value given to ‘x’ always satisfies the equation]
Similarly,
(b) (3a + 4) + 2 (a – 1) = 5a + 2
i.e., 5a + 2 = 5a + 2 (By simplification)
[any value given to ‘a’ always satisfies the equation]
The two expressions (LHS and RHS) are always equal for any value we give to the variable.
Equations that are true for any value of the variable are called Identical equations or Identities.
Solving Linear Equations
The process of finding the value of the unknown quantity for which the equation is true, is called
solving the equation. The value so found is called the root or solution of the equation.
The process of solving a simple equation depends upon the following axioms:
Addition Property
If any number is added to both sides of an equation, then the equality of the equation remains
unchanged.
i.e., if x = y then x + a = y + a
Subtraction Property
If any number is subtracted from both sides of an equation, then the equality of 0the equation
remains unchanged.
i.e., if x = y, then x – a = y – a
Multiplication and Division Property
The following are also true.
where a is a non-zero constant.
Graphical representation of a Linear Equation in one variable
Rectangular Axes
The position of a point in a plane is fixed by selecting two axes of reference which are formed by
combining two number lines at right angles so that their zeros coincide.
The horizontal number line is called the x-axis and the vertical number line is called y-axis.
The point of intersection of the two number lines is called origin.
The two number lines together are called rectangular axes.
Coordinates
The position of a point concerning the rectangular axes using a pair of numbers is
called coordinates.
The distance OM of point P along x-axis is called x-coordinate or abscissa.
The distance ON of point P along y-axis is called ordinate or y-coordinate.
If OM=a and ON=b then position of the point P is denoted by (a, b).
Coordinates of the origin is (0, 0).
Coordinates of any point on the x-axis is (x, 0).
Coordinates of any point on the y-axis is (0, y).
Quadrants
The rectangular axes divide the plane into four regions called quadrants.
By convention the quadrants are numbered as I, II, III, IV in the anti-clockwise direction.
In the I quadrant, any point will have both the coordinates positive.
In the II quadrant, x-coordinate is negative while y-coordinate is positive.
In the III quadrant, both x-coordinate and y-coordinate are negative.
In the IV quadrant, x-coordinate is positive while the y-coordinate is negative.
To Plot the Graph of a Linear Equation in one Variable
ax + b = 0 is a linear equation in one variable.
Consider the equation 2x + 4 = 0
2x = -4
x = -2
Since this equation is independent of y, for all values of y, x = -2
Hence x = -2 is a line parallel to the y-axis at x = -2.
Consider the equation y – 5 = 0
y – 5 = 0
y = 5
Since this equation is independent of x, for all values of x, y = 5.
Hence the graph of y = 5 is a line parallel to the x-axis at y = 5.
The graph of x = a is a line parallel to y-axis at x=a. The graph of y=b is a line parallel to x-axis
at y = b.
Linear equations in two variables
A linear equation in two variables is of the form ax + by = c, where
Example:
2x + 3y = 5, x – 2y = 6, -6x + y =8
A pair of values of x and y that satisfy a given linear equation in two variables is said to be its
solution.
Graph of a Linear Equation in two variables
To plot the graph of a linear equation in two variables
Re-write the given equation expressing one term in terms of the other.
Draw the x and y – axes. Choose a suitable scale to locate the selected point on the
graph.
Plot the selected points.
Draw a straight line joining the points.
NCERT Solutions For Class 9th Linear Equations In Two Variables
Ex 4.1 Class 9 Maths Question 1.
The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.
(Take the cost of a notebook to be Rs. x and that of a pen to be Rs.y).
Solution:
Let the cost of a notebook = Rs. x
and the cost of a pen = Rs. y
According to the condition, we have
[Cost of a notebook] =2 x [Cost of a pen]
i. e„ (x) = 2 x (y) or, x = 2y
or, x – 2y = 0
Thus, the required linear equation is x – 2y = 0.
Ex 4.1 Class 9 Maths Question 2
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
(i) 2x + 3y = 9.35¯¯¯
(ii) x−y5−10=0
(iii) – 2x + 3y = 6
(iv) x = 3y
(v) 2x = -5y
(vi) 3x + 2 = 0
(vii) y – 2 = 0
(viii) 5 = 2x
Solution:
(i) We have 2x + 3y = 9.35¯¯¯
or (2)x + (3)y + (−9.35¯¯¯ ) = 0
Comparing it with ax + by +c= 0, we geta = 2,
b = 3 and c= –9.35¯¯¯ .
(ii) We have x−y5−10=0
or x + (- 15) y + (10) = 0
Comparing it with ax + by + c = 0, we get
a =1, b =- 15 and c= -10
(iii) Wehave -2x + 3y = 6 or (-2)x + (3)y + (-6) = 0
Comparing it with ax – 4 – by + c = 0,we get a = -2, b = 3 and c = -6.
(iv) We have x = 3y or (1)x + (-3)y + (0) = 0 Comparing it with ax + by + c = 0, we get a = 1, b = -3 and c = 0.
(v) We have 2x = -5y or (2)x + (5)y + (0) = 0 Comparing it with ax + by + c = 0, we get a = 2, b = 5 and c = 0.
(vi) We have 3x + 2 = 0 or (3)x + (0)y + (2) = 0 Comparing it with ax + by + c = 0, we get a = 3, b = 0 and c = 2.
(vii) We have y – 2 = 0 or (0)x + (1)y + (-2) = 0 Comparing it with ax + by + c = 0, we get a = 0, b = 1 and c = -2.
(viii) We have 5 = 2x ⇒ 5 – 2x = 0
or -2x + 0y + 5 = 0
or (-2)x + (0)y + (5) = 0
Comparing it with ax + by + c = 0, we get a = -2, b = 0 and c = 5.
NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.2
Question 1
Which one of the following options is true, and why?
y = 3x + 5 has
(i) a unique solution,
(ii) only two solutions,
(iii) infinitely many solutions
Solution:
Option (iii) is true because for every value of x, we get a corresponding value of y and vice-versa in the given equation.
Hence, given linear equation has an infinitely many solutions.
Question 2
Write four solutions for each of the following equations:
(i) 2x + y = 7
(ii) πx + y = 9
(iii) x = 4y
Solution:
(i) 2x + y = 7
When x = 0, 2(0) + y = 7 ⇒ y = 7
∴ Solution is (0, 7)
When x =1, 2(1) + y = 7 ⇒ y = 7 – 2 ⇒ y = 5
∴ Solution is (1, 5)
When x = 2, 2(2) + y =7y = 7 – 4 ⇒ y = 3
∴ Solution is (2, 3)
When x = 3, 2(3) + y = 7y = 7 – 6 ⇒ y = 1
∴ Solution is (3, 1).
(ii) πx + y = 9
When x = 0, π(0) + y = 9 ⇒ y = 9 – 0 ⇒ y = 9
∴ Solution is (0, 9)
When x = 1, π(1) + y = 9 ⇒ y = 9 – π
∴ Solution is (1, (9 – π))
When x = 2, π(2) + y = 9 ⇒ y = 9 – 2π
∴ Solution is (2, (9 – 2π))
When x = -1,π(-1) + y = 9 ⇒ y = 9 + π
∴ Solution is (-1, (9 + π))
(iii) x = 4y
When x = 0, 4y = 1 ⇒ y = 0
∴ Solution is (0, 0)
When x = 1, 4y = 1 ⇒ y = 14
∴ Solution is (1,14 )
When x = 4, 4y = 4 ⇒ y = 1
∴ Solution is (4, 1)
When x = 4, 4y = 4 ⇒ y = -1
∴ Solution is (-4, -1)
Check which of the following are solutions of the equation x – 2y = 4 and which are not:
(i) (0,2)
(ii) (2,0)
(iii) (4, 0)
(iv) (√2, 4√2)
(v) (1, 1)
Solution:
(i) (0,2) means x = 0 and y = 2
Puffing x = 0 and y = 2 in x – 2y = 4, we get
L.H.S. = 0 – 2(2) = -4.
But R.H.S. = 4
∴ L.H.S. ≠ R.H.S.
∴ x =0, y =2 is not a solution.
(ii) (2, 0) means x = 2 and y = 0
Putting x = 2 and y = 0 in x – 2y = 4, we get
L.H:S. 2 – 2(0) = 2 – 0 = 2.
But R.H.S. = 4
∴ L.H.S. ≠ R.H.S.
∴ (2,0) is not a solution.
(iii) (4, 0) means x = 4 and y = 0
Putting x = 4 and y = o in x – 2y = 4, we get
L.H.S. = 4 – 2(0) = 4 – 0 = 4 =R.H.S.
∴ L.H.S. = R.H.S.
∴ (4, 0) is a solution.
(iv) (√2, 4√2) means x = √2 and y = 4√2
Putting x = √2 and y = 4√2 in x – 2y = 4, we get
L.H.S. = √2 – 2(4√2) = √2 – 8√2 = -7√2
But R.H.S. = 4
∴ L.H.S. ≠ R.H.S.
∴ (√2 , 4√2) is not a solution.
(v) (1, 1)means x =1 and y = 1
Putting x = 1 and y = 1 in x – 2y = 4, we get
LH.S. = 1 – 2(1) = 1 – 2 = -1. But R.H.S = 4
∴ LH.S. ≠ R.H.S.
∴ (1, 1) is not a solution.
Question 4
Find the value of k, if x = 2, y = 1 ¡s a solution of the equation 2x + 3y = k.
Solution:
We have 2x + 3y = k
putting x = 2 and y = 1 in 2x+3y = k,we get
2(2) + 3(1) ⇒ k = 4 + 3 – k ⇒ 7 = k
Thus, the required value of k is 7.
NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.3
Question 1
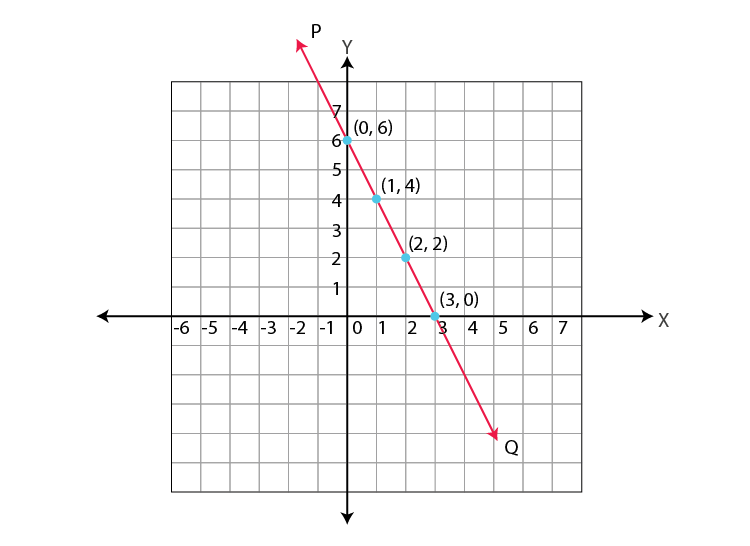
Draw the graph of each of the following linear equations in two variables:
(i) x + y = 4
(ii) x – y = 2
(iii) y = 3x
(iv) 3 = 2x + y
Solution:
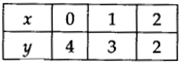
(i) x + y = 4 ⇒ y = 4 – x
If we have x = 0, then y = 4 – 0 = 4
x = 1, then y =4 – 1 = 3
x = 2, then y = 4 – 2 = 2
∴ We get the following table:
Plot the ordered pairs (0, 4), (1,3), and (2,2) on the graph paper. Joining these points, we get a straight line AB as shown.
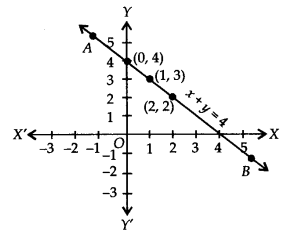
Thus, the line AB is the required graph of x + y = 4
(ii) x – y = 2 ⇒ y = x – 2
If we have x = 0, then y = 0 – 2 = -2
x = 1, then y = 1 – 2 = -1
x = 2, then y = 2 – 2 = 0
∴ We get the following table:
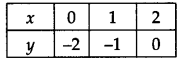
Plot the ordered pairs (0, -2), (1, -1) and (2, 0) on the graph paper. Joining these points, we get a straight line PQ as shown.
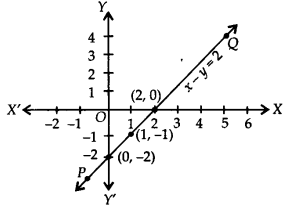
Thus, the time is the required graph of x – y = 2
(ii) x – y = 2 ⇒ y = x – 2
If we have x = 0, then y = 0 – 2 = -2
x = 1, then y = 1 – 2 = -1
x = 2, then y = 2 – 2 = 0
∴ We get the following table:
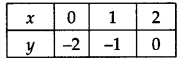
Plot the ordered pairs (0, -2), (1, -1) and (2, 0) on the graph paper. Joining these points, we get a straight line PQ as shown.
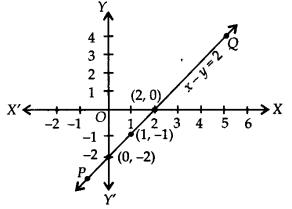
Thus, the time is the required graph of x – y = 2
If we have x = 0,
then y = 3(0) ⇒ y = 0
x = 1, then y = 3(1) = 3
x= -1, then y = 3(-1) = -3
∴ We get the following table:
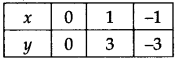
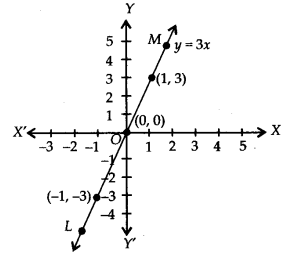
Thus, the line LM is the required graph of y = 3x.
(iv) 3 = 2x + y ⇒ y = 3 – 2x
If we have x = 0, then y = 3 – 2(0) = 3
x = 1,then y = 3 – 2(1) = 3 – 2 = 1
x = 2,then y = 3 – 2(2) = 3 – 4 = -1
∴ We get the following table:

Plot the ordered pairs (0, 3), (1, 1) and (2, – 1) on the graph paper. Joining these points, we get a straight line CD as shown.
Thus, the line CD is the required graph of 3 = 2x + y.
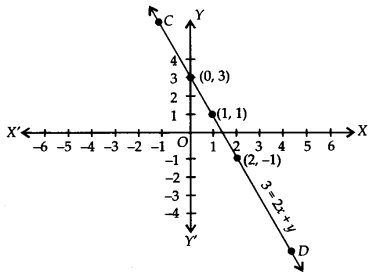
Question 2
Give the equations of two lines passing through (2, 14). How many more such lines are there, and why?
Solution:
(2, 14) means x = 2 and y = 14
Equations which have (2,14) as the solution are (i) x + y = 16, (ii) 7x – y = 0
There are infinite number of lines which passes through the point (2, 14), because infinite number of lines can be drawn through a point.
Question 3
If the point (3, 4) lies on the graph of the equation 3y = ax + 7, find the value of a.
Solution:
The equation of the given line is 3y = ax + 7
∵ (3, 4) lies on the given line.
∴ It must satisfy the equation 3y = ax + 7
We have, (3, 4) ⇒ x = 3 and y = 4.
Putting these values in given equation, we get
3 x 4 = a x 3 + 7
⇒ 12 = 3a + 7
⇒ 3a = 12 – 7 = 5 ⇒ a = 53
Thus, the required value of a is 53
Question 4
The taxi fare In a city Is as follows: For the first kilometre, the fare Is Rs. 8 and for the subsequent distance it is Rs. 5 per km. Taking the distance covered as x km and total fare as Rs.y, write a linear equation for this Information, and draw Its graph.
Solution:
Here, total distance covered = x km and total taxi fare = Rs. y
Fare for 1km = Rs. 8
Remaining distance = (x – 1) km
∴ Fare for (x – 1)km = Rs.5 x(x – 1)
Total taxi fare = Rs. 8 + Rs. 5(x – 1)
According to question,
y = 8 + 5(x – 1) = y = 8 + 5x – 5
⇒ y = 5x + 3,
which is the required linear equation representing the given information.
Graph: We have y = 5x + 3
When x = 0, then y = 5(0) + 3 ⇒ y = 3
x = 0, then y = 5(0) + 3 ⇒ y = 3
x = -1, then y = 5(-1) + 3 ⇒ y = -2
x = -2, then y = 5(-2) + 3 ⇒ y = -7
∴ We get the following table:
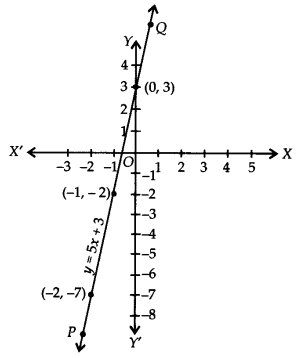
Thus, the line PQ is the required graph of the linear equation y = 5x + 3.
Question 5
From the choices given below, choose the equation whose graphs are given ¡n Fig. (1) and Fig. (2).
For Fig. (1)
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x
For Fig. (2)
(i) y = x + 2
(ii) y = x – 2
(iii) y = -x + 2
(iv) x + 2y = 6
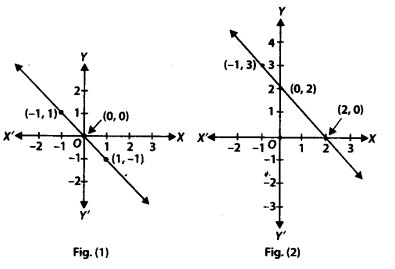
Solution:
For Fig. (1), the correct linear equation is x + y = 0
[As (-1, 1) = -1 + 1 = 0 and (1,-1) = 1 + (-1) = 0]
For Fig.(2), the correct linear equation is y = -x + 2
[As(-1,3) 3 = -1(-1) + 2 = 3 = 3 and (0,2)
⇒ 2 = -(0) + 2 ⇒ 2 = 2]
Question 6
If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance travelled by the body is
(i) 2 units
(ii) 0 unit
Solution:
Constant force is 5 units.
Let the distance travelled = x units and work done = y units.
Work done = Force x Distance
⇒ y = 5 x x ⇒ y = 5x
For drawing the graph, we have y = 5x
When x = 0, then y = 5(0) = 0
x = 1, then y = 5(1) = 5
x = -1, then y = 5(-1) = -5
∴ We get the following table:
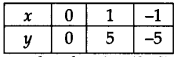
Ploffing the ordered pairs (0, 0), (1, 5) and (-1, -5) on the graph paper and joining the points, we get a straight line AB as shown.
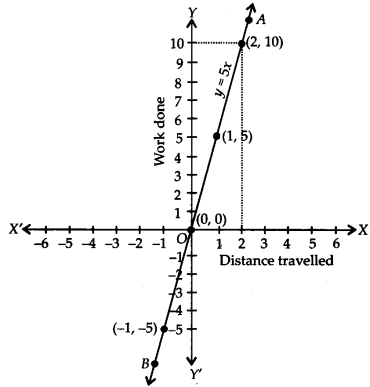
From the graph, we get
(i) Distance travelled =2 units i.e., x = 2
∴ If x = 2, then y = 5(2) = 10
⇒ Work done = 10 units.
(ii) Distance travelled = 0 unit i.e., x = 0
∴ If x = 0 ⇒ y = 5(0) – 0
⇒ Work done = 0 unit.
Question 7
Yamini and Fatima, two students of Class IX of a school, together contributed Rs. 100 towards the Prime Minister’s Relief Fund to help the earthquake victims. Write a linear equation which satisfies this data. (You may take their contributions as Rs.xand Rs.y.) Draw the graph of the same.
Solution:
Let the contribution of Yamini = Rs. x
and the contribution of Fatima Rs. y
∴ We have x + y = 100 ⇒ y = 100 – x
Now, when x = 0, y = 100 – 0 = 100
x = 50, y = 100 – 50 = 50
x = 100, y = 100 – 100 = 0
∴ We get the following table:

Plotting the ordered pairs (0,100), (50,50) and (100, 0) on a graph paper using proper scale and joining these points, we get a straight line PQ as shown.
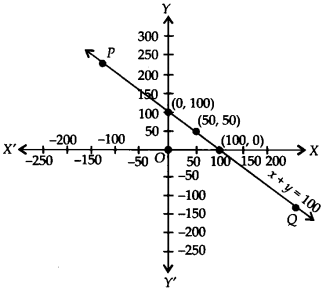
Thus, the line PQ is the required graph of the linear equation x + y = 100.
Question 8
In countries like USA and Canada, temperature is measured In Fahrenheit, whereas in countries like India, it is measured in Celsius. Here Is a
linear equation that converts Fahrenheit to Celsius:
F = (95 )C + 32
(i) Draw the graph of the linear equation above using Celsius for x-axis and Fahrenheit for y-axis.
(ii) If the temperature Is 30°C, what is the temperature in Fahrenheit?
(iii) If the temperature is 95°F, what is the temperature in Celsius?
(iv) If the temperature is 0°C, what Is the temperature In Fahrenheit and If the temperature is 0°F, what Is the temperature In Celsius?
(v) Is there a temperature which is numerically the same in both Fahrenheit and Celsius? If yes, find It.
Solution:
(i) We have
F = (95 )C + 32
When C = 0 , F = (95 ) x 0 + 32 = 32
When C = 15, F = (95 )(-15) + 32= -27 + 32 = 5
When C = -10, F = 95 (-10)+32 = -18 + 32 = 14
We have the following table:
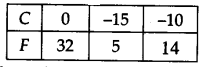
Plotting the ordered pairs (0, 32), (-15, 5) and (-10,14) on a graph paper. Joining these points, we get a straight line AB.
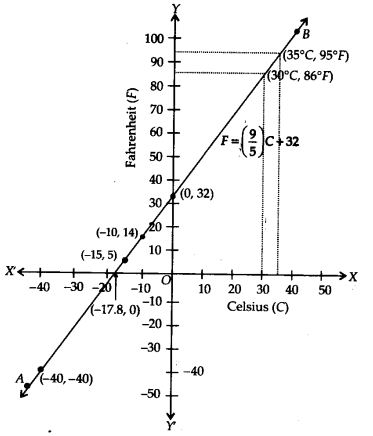
(ii) From the graph, we have 86°F corresponds to 30°C.
(iii) From the graph, we have 95°F corresponds 35°C.
(iv) We have, C = 0
From (1), we get
F = (95)0 + 32 = 32
Also, F = 0
From (1), we get
0 = (95)C + 32 ⇒ −32×59 = C ⇒ C = -17.8
(V) When F = C (numerically)
From (1), we get
F = 95F + 32 ⇒ F – 95F = 32
⇒ −45F = 32 ⇒ F = -40
∴ The temperature is – 40° both in F and C.
NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.4
Question 1
Give the geometric representations of y = 3 as an equation
(i) in one variable
(ii) in two variables
Solution:
(i) y = 3
∵ y = 3 is an equation in one variable, i.e., y only.
∴ y = 3 is a unique solution on the number line as shown below:
(ii) y = 3
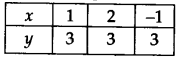
We can write y = 3 in two variables as 0.x + y = 3
Now, when x = 1, y = 3
x = 2, y = 3
x = -1, y = 3
∴ We get the following table:
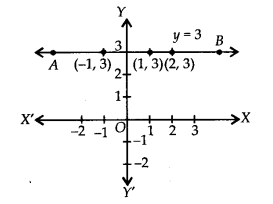
Plotting the ordered pairs (1, 3), (2, 3) and (-1, 3) on a graph paper and joining them, we get aline AB as solution of 0. x + y = 3,
i.e. y = 3.
Question 2
Give the geometric representations of 2x + 9 = 0 as an equation
(i) in one variable
(ii) in two variables
Solution:
(i) 2x + 9 = 0
We have, 2x + 9 = 0 ⇒ 2x = – 9 ⇒ x = −92
which is a linear equation in one variable i.e., x only.
Their are, x = −92 is a unique solution on the number line as shown below:
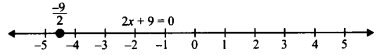
Conclusion
We hope the NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables helped you. If you still have any queries regarding NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables, you can stay in touch with us.
Related Articles
